5.408. two_orth_are_in_contact
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
[Roach84], used for defining .
- Constraint
- Type
- Arguments
- Restrictions
- Purpose
Enforce the following conditions on two orthotopes and :
For all dimensions , except one dimension, the projections of and onto have a non-empty intersection.
For all dimensions , the distance between the projections of and onto is equal to 0.
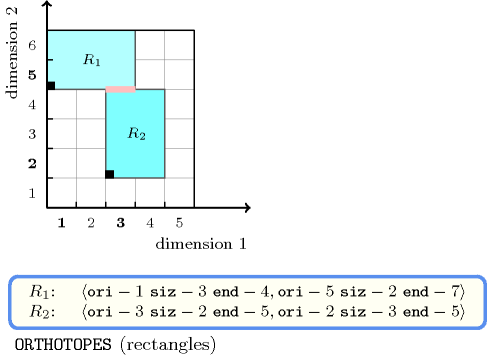
- Example
-
Figure 5.408.1 shows the two rectangles of the example. The constraint holds since the two rectangles are in contact: the contact is depicted by a pink line-segment.
Figure 5.408.1. The two rectangles that are in contact of the Example slot where the contact is shown in pink
- Typical
- Symmetries
Arguments are permutable w.r.t. permutation .
Items of and are permutable (same permutation used).
- Used in
- See also
implies: .
- Keywords
characteristic of a constraint: automaton, automaton without counters, reified automaton constraint.
constraint network structure: Berge-acyclic constraint network.
geometry: geometrical constraint, touch, contact, non-overlapping, orthotope.
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
-
- Graph property(ies)
-
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
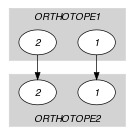
- Graph model
Parts (A) and (B) of Figure 5.408.2 respectively show the initial and final graph associated with the first graph constraint of the Example slot. Since we use the graph property, the unique arc of the final graph is stressed in bold. It corresponds to the fact that the projection onto dimension 1 of the two rectangles of the example overlap.
Figure 5.408.2. Initial and final graph of the constraint
(a) (b) - Signature
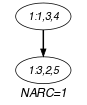
Consider the second graph constraint. Since we use the arc generator on the collections and , and because of the restriction , the maximum number of arcs of the corresponding final graph is equal to . Therefore we can rewrite the graph property to and simplify to .
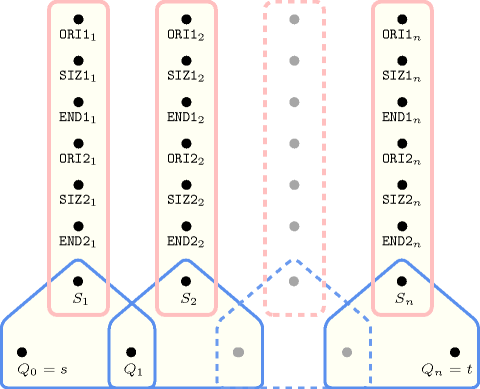
- Automaton
Figure 5.408.3 depicts the automaton associated with the constraint. Let , and respectively be the , the and the attributes of the item of the collection. Let , and respectively be the , the and the attributes of the item of the collection. To each sextuple corresponds a signature variable , which takes its value in , as well as the following signature constraint:
.
Figure 5.408.3. Automaton of the constraint
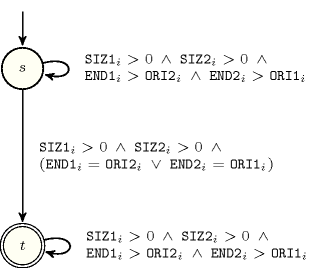
Figure 5.408.4. Hypergraph of the reformulation corresponding to the automaton of the constraint