5.264. minimum_greater_than
| DESCRIPTION | LINKS | GRAPH | AUTOMATON |
- Origin
N. Beldiceanu
- Constraint
- Arguments
- Restrictions
- Purpose
is the smallest value strictly greater than of the collection of variables : this concretely means that there exists at least one variable of that takes a value strictly greater than .
- Example
-
The constraint holds since value 5 is the smallest value strictly greater than value 3 among values and 8.
- Typical
- Symmetry
Items of are permutable.
- Arg. properties
Aggregate: , , .
- Reformulation
Let denote the variables of the collection of variables . By creating the extra variables and , the constraint can be expressed in term of the following constraints:
- See also
common keyword: (order constraint).
related: (identify an element in a table).
- Keywords
characteristic of a constraint: minimum, automaton, automaton without counters, reified automaton constraint, derived collection.
constraint network structure: centered cyclic(2) constraint network(1).
- Derived Collection
- Arc input(s)
- Arc generator
-
- Arc arity
- Arc constraint(s)
- Graph property(ies)
-
- Sets
-
- Constraint(s) on sets
- Graph model
Similar to the constraint, except that there is no order on the variables of the collection .
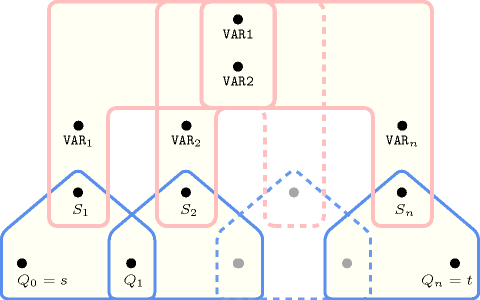
Parts (A) and (B) of Figure 5.264.1 respectively show the initial and final graph associated with the Example slot. Since we use the graph property, the arcs of the final graph are stressed in bold. The source and the sinks of the final graph respectively correspond to the variable and to the variables of the collection that are strictly greater than . is set to the smallest value of the attribute of the sinks of the final graph.
Figure 5.264.1. Initial and final graph of the constraint
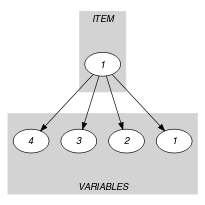
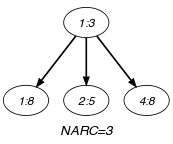
(a) (b)
- Automaton
Figure 5.264.2 depicts the automaton associated with the constraint. Let be the variable of the collection. To each triple corresponds a signature variable as well as the following signature constraint:
.
The automaton is constructed in order to fulfil the following conditions:
We look for an item of the collection such that and ,
There should not exist any item of the collection such that and .
Figure 5.264.2. Automaton of the constraint
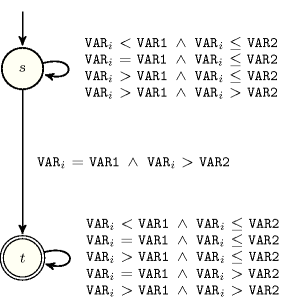
Figure 5.264.3. Hypergraph of the reformulation corresponding to the counter free non deterministic automaton of the constraint