5.54. bin_packing_capa
| DESCRIPTION | LINKS |
- Origin
- Constraint
- Arguments
- Restrictions
- Purpose
Given several items of the collection (each of them having a specific weight), and different bins described the the items of collection (each of them having a specific capacity ), assign each item to a bin so that the total weight of the items in each bin does not exceed the capacity of the bin.
- Example
-
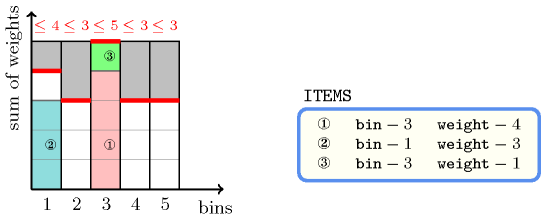
The constraint holds since the sum of the height of items that are assigned to bins 1 and 3 is respectively equal to 3 and 5. The previous quantities are respectively less than or equal to the maximum capacities 4 and 5 of bins 1 and 3. Figure 5.54.1 shows the solution associated with the example.
Figure 5.54.1. Bin-packing solution to the Example slot
- Typical
- Symmetries
Items of are permutable.
Items of are permutable.
can be increased.
can be decreased to any value .
All occurrences of two distinct values in or can be swapped; all occurrences of a value in or can be renamed to any unused value.
- Arg. properties
Contractible wrt. .
- Remark
In MiniZinc (http://www.minizinc.org/) there is also a constraint called which, for each bin has a domain variable that is equal to the sum of the weights assigned to the corresponding bin.
- Systems
pack in Choco, binpacking in Gecode, bin_packing_capa in MiniZinc.
- See also
generalisation: (negative contribution also allowed).
specialisation: (non-fixed capacity replaced by fixed overall capacity).
- Keywords
-
constraint type: predefined constraint, resource constraint.
modelling: assignment dimension, assignment to the same set of values.