Global Constraint Catalog: Csoft_same_interval

5.362. soft_same_interval_var

DESCRIPTION

LINKS

GRAPH

Origin

Derived from $𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$

Constraint

$𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛 (𝙲, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$

Synonym

$𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

Arguments

$𝙲$	$𝚍𝚟𝚊𝚛$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$	$𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛 - 𝚍𝚟𝚊𝚛)$
$𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$	$𝚒𝚗𝚝$

Restrictions

𝙲 \geq 0

𝙲 \leq | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 |

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | = | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 |

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚟𝚊𝚛)

𝚛𝚎𝚚𝚞𝚒𝚛𝚎𝚍

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2, 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 0

Purpose

Let $N_{i}$ (respectively $M_{i}$ ) denote the number of variables of the collection $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ (respectively $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ ) that take a value in the interval $[𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot i, 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \cdot i + 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 - 1$ . $𝙲$ is the minimum number of values to change in the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections so that for all integer $i$ we have $N_{i} = M_{i}$ .

Example

(4, 〈9, 9, 9, 9, 9, 1〉, 〈9, 1, 1, 1, 1, 8〉, 3)

In the example, the fourth argument $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = 3$ defines the following family of intervals $[3 \cdot k, 3 \cdot k + 2]$ , where $k$ is an integer. Consequently the values of the collections $〈 9, 9, 9, 9, 9, 1 〉$ and $〈 9, 1, 1, 1, 1, 8 〉$ are respectively located within intervals $[9, 11]$ , $[9, 11]$ , $[9, 11]$ , $[9, 11]$ , $[9, 11]$ , $[0, 2]$ and intervals $[9, 11]$ , $[0, 2]$ , $[0, 2]$ , $[0, 2]$ , $[0, 2]$ , $[6, 8]$ . Since there is a correspondence between two pairs of intervals we must unset at least $6 - 2$ items (6 is the number of items of the $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ collections). Consequently, the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ constraint holds since its first argument $𝙲$ is set to $6 - 2$ .

Typical

𝙲 > 0

| 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛) > 1

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛) > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 > 1

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛)

𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 <

𝚛𝚊𝚗𝚐𝚎

(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛)

Symmetries

Arguments are permutable w.r.t. permutation $(𝙲)$ $(𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1, 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2)$ $(𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻)$ .
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ are permutable.
Items of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$ are permutable.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.
An occurrence of a value of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2 . 𝚟𝚊𝚛$ that belongs to the $k$ -th interval, of size $𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻$ , can be replaced by any other value of the same interval.

Usage

A soft $𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ constraint.

Algorithm

See algorithm of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚟𝚊𝚛$ constraint.

See also

hard version: $𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕$ .

implies: $𝚜𝚘𝚏𝚝_𝚞𝚜𝚎𝚍_𝚋𝚢_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ .

Keywords

constraint arguments: constraint between two collections of variables.

constraint type: soft constraint, relaxation, variable-based violation measure.

modelling: interval.

Arc input(s)

$𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 2$

Arc generator

𝑃𝑅𝑂𝐷𝑈𝐶𝑇

\mapsto 𝚌𝚘𝚕𝚕𝚎𝚌𝚝𝚒𝚘𝚗 (𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1, 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2)

Arc arity

Arc constraint(s)

\begin{matrix} 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 1 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 = \\ 𝚟𝚊𝚛𝚒𝚊𝚋𝚕𝚎𝚜 2 . 𝚟𝚊𝚛 / 𝚂𝙸𝚉𝙴_𝙸𝙽𝚃𝙴𝚁𝚅𝙰𝙻 \end{matrix}

Graph property(ies)

𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄

= | 𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1 | - 𝙲

Graph model

Parts (A) and (B) of Figure 5.362.1 respectively show the initial and final graph associated with the Example slot. Since we use the $𝐍𝐒𝐈𝐍𝐊_𝐍𝐒𝐎𝐔𝐑𝐂𝐄$ graph property, the source and sink vertices of the final graph are stressed with a double circle. The $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ constraint holds since the cost 4 corresponds to the difference between the number of variables of $𝚅𝙰𝚁𝙸𝙰𝙱𝙻𝙴𝚂 1$ and the sum over the different connected components of the minimum number of sources and sinks.

Figure 5.362.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ constraint

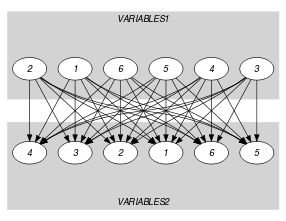
(a)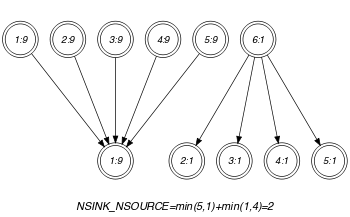

(b)

Global Constraint Catalog

5. Global Constraint Catalogue

5.362. soft_same_interval_var

Figure 5.362.1. Initial and final graph of the 𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛 constraint

Figure 5.362.1. Initial and final graph of the $𝚜𝚘𝚏𝚝_𝚜𝚊𝚖𝚎_𝚒𝚗𝚝𝚎𝚛𝚟𝚊𝚕_𝚟𝚊𝚛$ constraint